Geometri Euclidean adalah sistem matematika yang dikaitkan dengan Alexandria matemati kawan Yunani Euclid , yang dijelaskan dalam buku teks tentang geometri yaitu Elements . Metode Euclid terdiri dalam asumsi satu set kecil intuitif menarik aksioma , dan menyimpulkan lainnya proposisi ( dalil ) dari ini. Meskipun banyak dari hasil Euclid telah dinyatakan oleh matematikawan sebelumnya, Euclid adalah yang pertama untuk menunjukkan bagaimana proposisi-proposisi bisa masuk ke dalam deduktif dan komprehensif sistem logis . Unsur dimulai dengan pesawat geometri, masih diajarkan di sekolah menengah sebagai yang pertama sistem aksiomatikdan contoh pertama dari bukti formal . Berpindah ke geometri solid dari tiga dimensi . Banyak dari Elemenmenyatakan hasil dari apa yang sekarang disebut aljabar dan nomor teori , ditulis dalam bahasa geometris.
Selama lebih dari dua ribu tahun, kata sifat "Euclid" tidak diperlukan karena tidak ada geometri lain yang disusun. Aksioma Euclid nampak seperti sangat jelas bahwa pembuktian teorema lainnya dianggap benar dalam arti, mutlak sering metafisik,. Namun, sekarang banyak lainnya konsisten diri non-Euclidean geometridiketahui, yang pertama yang telah ditemukan pada awal abad 19. Implikasi dari Einstein teori relativitas umum adalah bahwa ruang Euclidean adalah pendekatan yang baik terhadap sifat ruang fisik hanya di mana medan gravitasi tidak terlalu kuat.
Unsur
Unsur terutama sebuah sistematisasi pengetahuan awal geometri. Keunggulannya di atas perawatan sebelumnya dengan cepat diakui, dengan hasil bahwa ada sedikit minat dalam melestarikan yang sebelumnya, dan mereka sekarang hampir semua hilang.
Buku I-IV dan VI membahas geometri bidang datar. Banyak hasil tentang tokoh-tokoh pesawat terbukti, misalnya, Jika segitiga memiliki dua sudut yang sama, maka sisi yang bersesuaian dengan sudut tersebut adalah sama . Teorema Pythagoras terbukti.
Buku V dan VII-X berurusan dengan nomor teori, dengan nomor diperlakukan secara geometris melalui representasi mereka sebagai segmen garis dengan berbagai panjang. Pengertian seperti bilangan prima danrasional dan bilangan irasional diperkenalkan. Yang tak terbatas bilangan prima terbukti.
Buku XI-XIII geometri perhatian padat. Hasil khas adalah rasio 01:03 antara volume kerucut dan silinder dengan ketinggian yang sama dan basis.

Persamaan postulat: Jika dua garis berpotongan sepertiga sedemikian rupa sehingga jumlah dari sudut-sudut bagian dalam di satu sisi kurang dari dua sudut yang tepat, maka mau tidak mau harus dua baris saling berpotongan pada sisi jika diperpanjang cukup jauh.
Aksioma
Geometri Euclidean adalah sistem aksiomatik , di mana semua teorema ("pernyataan benar") berasal dari sejumlah kecil aksioma. Menjelang awal buku pertama dari Elemen, Euclid memberikan lima postulat(aksioma) untuk pesawat geometri , menyatakan dalam hal konstruksi (sebagaimana diterjemahkan oleh Thomas Heath):
"Mari berikut akan mendalilkan":
1. "Untuk menggambar garis lurus dari setiap titikke titik apapun. "
2. "Untuk menghasilkan [memperluas] sebuah garis lurus yang terbatas terus menerus dalam garis lurus. "
3. "Untuk menggambarkan lingkaran dengan pusat dan jarak [radius]. "
4. "Itu semua sudut yang tepat sama dengan satu sama lain."
5. Para paralel dalil : "Itu, jika garis lurus jatuh di dua jalur lurus membuat sudut interior pada sisi yang sama kurang dari dua sudut yang tepat, dua garis lurus, jika diproduksi tanpa batas waktu, bertemu di sisi itu yang adalah sudut kurang dari dua sudut yang tepat. "
Meskipun pernyataan Euclid dari postulat hanya secara eksplisit menegaskan keberadaan konstruksi, mereka juga diambil untuk menjadi unik.
Elements juga memasukkan lima "notasi biasa":
1. Hal-hal yang sama dengan hal yang sama juga sama satu dengan lainnya.
2. Jika sesuatu yang sama ditambahkan ke sama, maka keutuhan adalah sama.
3. Jika sesuatu yang sama dikurangkan dari sama, maka sisanya adalah sama.
4. Hal-hal yang bertepatan dengan satu sama lain sama satu sama lain.
5. Keseluruhan lebih besar daripada bagian.
Paralel postulat
Untuk nenek moyang, paralel tampak kurang jelasmendalilkan dari yang lain. Euclid sendiri tampaknya telah dianggap sebagai yang secara kualitatif berbeda dari yang lain, sebagaimana dibuktikan oleh organisasi dari Elemen: 28 yang pertama ia menyajikan proposisi adalah mereka yang dapat dibuktikan tanpa itu.
Aksioma banyak alternatif dapat dirumuskan yang samakonsekuensi logis sebagai paralel dalil. Misalnyaaksioma Playfair 's menyatakan:
Dalam pesawat, melalui titik tidak pada garis lurus yang diberikan, paling banyak satu baris dapat ditarik bahwa tidak pernah memenuhi garis yang diberikan.
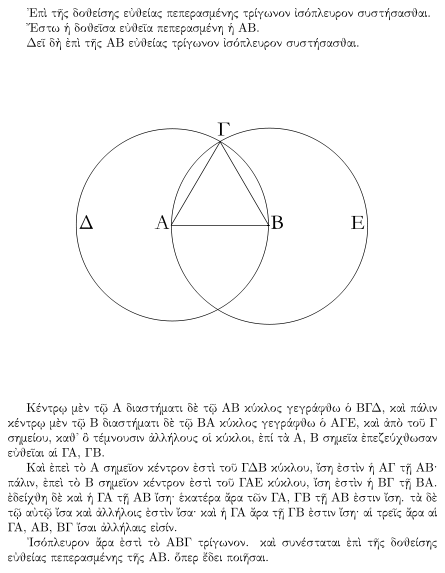
Sebuah bukti dari elemen Euclid bahwa, mengingat segmen garis, segitiga sama sisi ada yang mencakup segmen sebagai salah satu sisinya. Buktinya adalah dengan mengkonstruksi sebuah segitiga sama sisi ΑΒΓ dibuat dengan menggambar lingkaran dan Δ Ε berpusat pada poin Α dan Β, dan mengambil satu persimpangan lingkaran sebagai titik ketiga dari segitiga.
Metode pembuktian
Geometri Euclid adalah konstruktif . Postulat 1, 2, 3, dan 5 menegaskan bahwa keberadaan dan keunikan dari bidang geometri tertentu, dan penegasan ini adalah konstruksi alam: yaitu, kita tidak diberitahu bahwa sesuatu itu ada, tetapi juga kita diberikan metode untuk membuatnya dengan lebih dari satu tidak ada kompas dan lurus yang tidak bertanda . Dalam hal ini, geometri Euclid adalah lebih konkrit daripada kebanyakan sistem aksiomatik modern seperti teori set , dimana sering menegaskan keberadaan objek tanpa memberitahukan bagaimana mengkonstruksi mereka, atau menegaskan keberadaan objek yang tidak dapat dibangun dalam teori. Tepatnya, garis-garis pada kertas model dari objek didefinisikan dalam sistem formal, bukan contoh objek tersebut. Misalnya garis lurus Euclidean memiliki lebar atau tidak, tetapi setiap garis yang ditarik akan nyata . Meskipun hampir semua matematikawan modern yang mempertimbangkan metode nonconstructive hanya sebagai suara yang konstruktif, bukti konstruktif Euclid sering diartikan keliru sebagai metode nonconstructive misalnya, beberapa bukti Pythagorean nomor irasionalyang terlibat, yang biasanya diperlukan pernyataan seperti "Cari ukuran umum terbesar dari ... "
Euclid sering digunakan bukti oleh kontradiksi . Geometri Euclidean juga memungkinkan metode superposisi, di mana angka ditransfer ke titik lain di ruang angkasa. Misalnya, proposisi I.4, pada kongruensi segitiga dengan aksioma sisi-sudut-sisi, terbukti dengan memindahkan salah satu dari dua segitiga sehingga salah satu sisinya bertepatan dengan sisi segitiga sama lain, dan kemudian membuktikan bahwa sisi lain bertepatan juga . Beberapa perawatan modern menambahkan seperenam postulat, kekakuan segitiga, yang dapat digunakan sebagai alternatif untuk superposisi.
Sistem pengukuran dan aritmatika
Geometri Euclidean memiliki dua tipe dasar pengukuran: sudut dan jarak. Skala sudut adalah mutlak, dan Euclid menggunakan sudut yang tepat sebagai unit dasarnya, sehingga, misalnya, sebuah sudut 45 derajat akan disebut sebagai setengah dari sudut kanan. Skala jarak relatif, satu sewenang-wenang mengambil segmen garis dengan panjang tertentu sebagai unit, dan jarak lainnya disajikan dalam kaitannya dengan hal itu.
Sebuah garis dalam geometri Euclidean adalah modelgaris bilangan real . Sebuah segmen garis adalah bagian dari garis yang dibatasi oleh dua titik akhir, dan berisi setiap titik pada garis antara titik akhir. Penambahan diwakili oleh konstruksi di mana satu segmen garis akan disalin ke akhir dari suatu segmen garis untuk memperpanjang panjangnya, dan juga untuk pengurangan.
Pengukuran luas dan volume berasal dari jarak. Sebagai contoh, sebuah persegi panjang dengan lebar 3 dan panjang 4 memiliki luas yang mewakili produk, 12. Karena interpretasi geometris dari perkalian terbatas pada tiga dimensi, tidak ada cara langsung menafsirkan produk dari empat atau lebih angka, dan Euclid dihindari produk tersebut, meskipun mereka tersirat, misalnya, dalam bukti buku IX, proposisi 20.

Contoh kongruensi. Dua angka di sebelah kiri adalah kongruen, sementara yang ketiga adalah serupa kepada mereka. Angka terakhir adalah tidak. Perhatikan bahwa kongruensi mengubah beberapa sifat, seperti lokasi dan orientasi, tetapi membiarkan yang lain tidak berubah, seperti jarak dan sudut . Jenis kedua sifat ini disebutinvariants dan pelajaran itu adalah inti dari geometri.
Euclid mengacu pada sepasang garis, atau sepasang bangun planar atau padat, sebagai "sama" (ἴσος) jika panjang mereka, daerah, atau volume adalah sama, dan juga untuk sudut. Istilah lebih kuat " kongruen "mengacu pada ide bahwa bangun dengan seluruh ukuran yang sama dan bentuk sebagai bentuk lain. Atau, dua bangun yang kongruen jika bangun tersebut dapat dipindahkan di atas yang lain sehingga cocok dengan persis. (Flipping di atas diperbolehkan.) Jadi, misalnya, persegi panjang 2x6 dan 3x4 persegi panjang adalah sama tetapi tidak kongruen, dan huruf R adalah kongruen dengan bayangannya. Angka yang akan kongruen kecuali untuk ukuran mereka yang berbeda disebut sebagai serupa.
Notasi dan terminologi
Penamaan poin dan angka
Poin lazim diberi nama menggunakan huruf alfabet. Objek lainnya, seperti garis, segitiga, atau lingkaran, diberi nama dengan daftar cukup banyak poin untuk menjemput mereka keluar jelas dari angka yang relevan, misalnya, segitiga ABC biasanya akan menjadi segitiga dengan simpul pada titik-titik A, B, dan C .
sudut pelengkap dan penunjang
Sudut yang jumlahnya 90 derajat adalah sudut siku-siku disebut komplementer , sedangkan sudut yang jumlahnya 180 derajat adalah sudut lurus adalahtambahan (suplementer).
Versi Modern notasi Euclid
Dalam terminologi modern, sudut biasanya akan diukur dalam derajat atau radian .
Buku pelajaran sekolah modern sering mendefinisikan bangun terpisah yang disebut baris (tak terbatas), sinar(semi-infinite), dan segmen garis (panjang terbatas). Euclid, daripada membahas sebuah sinar sebagai objek yang meluas hingga tak terbatas dalam satu arah, biasanya akan menggunakan lokusi seperti "jika baris ini diperpanjang dengan panjang yang cukup," meskipun ia kadang-kadang disebut "garis yang tak terbatas." Sebuah "garis" dalam Euclid dapat berupa lurus atau melengkung, dan ia menggunakan istilah yang lebih spesifik "garis lurus" bila diperlukan.
Beberapa hasil penting atau terkenal


Jumlah dari sudut A, B, dan C adalah sama dengan 180 derajat.
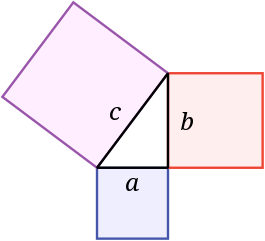
Teorema Pythagoras: Jumlah dari bidang dua kotak pada kaki (a dan b) dari sebuah segitiga siku-siku sama dengan luas persegi pada sisi miring (c).

Teorema Thales: jika AC adalah diameter, maka sudut di B adalah sudut kanan.
Jembatan Menilai
Jembatan menilai (Pons Asinorum) menyatakan bahwadalam segitiga sama kaki sudut di dasar sama satu sama lain, dan, jika garis-garis lurus yang sama yang diproduksi lebih lanjut, maka sudut bawah dasar sama satu sama lain. Namanya mungkin dikaitkan dengan peran sering sebagai tes nyata pertama dalam Unsur-unsur kecerdasan pembaca dan sebagai jembatan untuk proposisi keras yang diikuti. Hal ini juga mungkin dinamakan demikian karena kemiripannya sosok geometris untuk jembatan yang curam yang hanya seekor keledai yang dapat menyeberang.
Kongruensi segitiga

Kongruensi segitiga ditentukan dengan menentukan dua sisi dan sudut antara mereka (SAS), dua sudut dan sisi antara mereka (ASA) atau dua sudut dan sisi yang berdekatan sesuai (SSA). Menentukan dua sisi dan sudut yang berdekatan (SSA), bagaimanapun, dapat menghasilkan dua segitiga yang mungkin berbeda.
Segitiga dikatakan kongruen jika mereka memiliki ketiga sisi yang sama (SSS), dua sisi dan sudut antara mereka sama (SAS), atau dua sudut dan sisi yang sama (ASA) (Buku I, proposisi 4, 8, dan 26). (Segitiga dengan tiga sudut yang sama umumnya serupa, tetapi belum tentu kongruen Juga, segitiga dengan dua sisi yang sama dan sudut yang berdekatan tidak selalu sama..)
Jumlah sudut sebuah segitiga
Jumlah sudut sebuah segitiga sama dengan sudut lurus (180 derajat).
Teorema Pythagoras
Para terkenal Teorema Pythagoras (buku I, proposisi 47) menyatakan bahwa dalam setiap segitiga siku-siku, luas persegi yang sisinya adalah sisi miring (sisi berlawanan sudut yang tepat) sama dengan jumlah dari bidang kotak yang sisi-sisinya bertemu di sudut 90 derajat (kedua belah pihak yang bertemu di sudut kanan).
Thales 'Teorema
Thales 'Teorema , yaitu setelah Thales dari Miletusmenyatakan bahwa jika A, B, dan C adalah titik pada lingkaran di mana garis AC adalah diameter lingkaran, maka sudut ABC adalah sudut kanan. Penyanyi menyangka bahwa Thales membuktikan Teorema melalui Euclid buku saya, prop 32 menurut cara Euclid buku III, prop 31. Tradisi mengatakan bahwa Thales mengorbankan lembu untuk merayakan teorema ini.
Scaling daerah dan volume
Dalam terminologi modern, area objek pesawat sebanding dengan kuadrat dari setiap dimensi linier. Dan volume yang solid untuk kubus. Euclid membuktikan hasil ini dalam berbagai kasus khusus seperti luas lingkaran dan volume yang solid parallelepipedal. Euclid ditentukan, tapi tidak semua, dari konstanta proporsionalitas yang relevan. Misalnya, itu penggantinya Archimedes yang membuktikan bahwa bola memiliki 2/3 volume silinder circumscribing.
Aplikasi
Karena status dasar geometri Euclidean dalam matematika, tidak mungkin untuk memberikan lebih dari sampling wakil dari aplikasi di sini.

Sebuah surveyor menggunakan Tingkat

Kemasan Sphere berlaku untuk tumpukan jeruk.

Sebuah cermin parabola membawa sinar paralel dari cahaya untuk fokus.
Seperti yang disarankan oleh etimologi kata, salah satu alasan paling awal untuk kepentingan dalam geometri itu survei , dan hasil praktis tertentu dari geometri Euclidean, seperti properti yang tepat-sudut segitiga 3-4-5, digunakan jauh sebelum mereka terbukti secara formal. Jenis-jenis dasar pengukuran dalam geometri Euclidean adalah jarak dan sudut, dan kedua kuantitas dapat diukur langsung oleh surveyor. Secara historis, jarak sering diukur dengan rantai seperti rantai Gunter itu , dan sudut menggunakan lingkaran lulus dan, kemudian, teodolit .
Sebuah aplikasi dari geometri Euclidean yang solid adalah penentuan pengaturan kemasan , seperti masalah untuk menemukan yang paling efisienkemasan bola dalam dimensi n. Masalah ini memiliki aplikasi dalam deteksi dan koreksi kesalahan .
Optik geometris menggunakan geometri Euclidean untuk menganalisis fokus cahaya oleh lensa dan cermin.

Geometri digunakan dalam seni dan arsitektur.

Menara air terdiri dari kerucut, silinder, dan setengah bola. Volumenya dapat dihitung dengan menggunakan geometri padat.

Geometri dapat digunakan untuk merancang origami.
Geometri digunakan secara luas dalam arsitektur .
Geometri dapat digunakan untuk merancang origami . Beberapa masalah konstruksi klasik geometri tidak mungkin menggunakan kompas dan penggaris-sejajar , tetapi dapat diselesaikan dengan menggunakan origami
Tidak ada komentar:
Posting Komentar